Gallery of Symmetries of Organisms

Organisms and their parts and products can have several symmetries, and this gallery is for illustrating them. This is a static gallery; for an interactive demo of rotational symmetries, try Organism-Symmetry Demo.

We say that something has a symmetry when it looks the same after some transformation, something that the above demo and 2D Point-Group Demo demonstrate. Symmetry transformations form abstract-algebra groups, meaning that performing two transformations creates another transformation, with this composition operation having three properties. It is associative (does not matter which pair to do first), it has an identity (transformation that does nothing), and every transformation has an inverse transformation, one that undoes it. This composition operation need not be commutative, however; different orders may give different results. Spatial transformations come in these categories:

Translations can be associated with rotations and reflections. They can be either

The most general n-dimensional space-transformation group is called the Euclidean group. It has these subgroups:

E(n) Translations, rotations, reflections
E(+,n), SE(n) Translations, rotations
T(n) Translations
O(n) Rotations, reflections
SO(n) Rotations

The groups O(n) and SO(n) are the most general n-dimensional point groups, groups that keep a point fixed.

The symmetries:

  1. One-Dimensional
    1. 1D point group: bilateral
    2. 1D space groups: line
    3. Helix
    4. Logarithmic spiral, cone
    5. Frieze
  2. Two-Dimensional
    1. 2D point groups: rosette
    2. Discrete 2D space groups: wallpaper
  3. Three-Dimensional
    1. 3D point groups: crystallographic
    2. Discrete 3D space groups: crystallographic
  4. Fractal

  1. One-Dimensional Symmetries

    One-dimensional symmetry group

    1. 1D point group: bilateral symmetry

      This is reflection without translation: O(1). It is usually left-right symmetry relative to the main body axis or structural axis.
      Cat Yawning: it is almost universal in the animal kingdom.
      Grape leaf: many plant leaves have this symmetry.

    2. 1D space groups: line

      Continuous with reflection: E(1), without reflection: SE(1) or T(1). Discrete wtih reflection: infinite dihedral D, without reflection: integers under addition Z.
      Dog hair: symmetry: ~ E(1). Scales are ~ Z, from their direction
      Corn plants: stem symmetry: SE(1). Leaf locations are Z, from their direction
      Canine roundworm: most of it outwardly has symmetry E(1)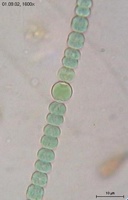
      Anabaena cyanobacterium: symmetry is the infinite dihedral D

    3. Helix

      Borrelia burgdorferi bacterium
      Diagram of DNA molecule

    4. Logarithmic spiral, cone

      Nautilus Shell
      Land-snail shell
      Conical snail shell

    5. Frieze groups

      The 7 frieze groups (Wikipedia) are discrete linear groups with additional symmetries in a second direction. They can be extended into three dimensions as the 13 infinite families of line groups, with 75 rod groups as regular-lattice subgroups. The previous discrete examples have mostly been p1, with Anabaena being p1m1.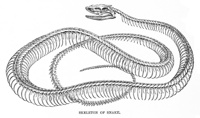
      Snake skeleton: vertebrates are segmented, with symmetry p11m
      House centipede: arthropods are segmented, with symmetry p11m
      Polychaete worm: annelids are segmented, with symmetry p11m
      Feather: around the shaft, the barbs have symmetry p11m
      Fern: The fronds have symmetry p11m to p11g
      Fern closeup: The leaflets also have symmetry p11m to p11g
      Cooked octopus: the suckers on the arms have symmetry p2mg

  2. Two-Dimensional Symmetries

    1. 2D point groups: rosette groups

      Point groups in two dimensions
      What Discrete (n-fold) Continuous
      Rotations C(n) - cyclic SO(2)
      Rot + Reflections D(n) - dihedral O(2)

      The number n is how many times to repeat a rotation before reaching the identity. The case n = 1 is degenerate; C(1) is the identity group, and D(1) is reflection only, like bilateral symmetry.

      They can be extended into three dimensions as the prismatic groups.

      Starfish: many starfish and other echinoderms have symmetry D(5)
      Octopus: arms have symmetry D(8)
      Squid: short arms have symmetry D(8), long arms D(2)
      Jellyfish: has symmetry D(4); other cnidarians have D(4), D(6) or D(8)
      Tribrachidium: has symmetry C(3) -- no reflections
      Mushroom: has symmetry O(2)
      Morning Glory: it and many other eudicot flowers have symmetry D(5)
      Poppy: some eudicot flowers have symmetry D(4)
      Sunflower: some eudicot flowers have symmetry D(large)
      Pansy: eudicot; flower symmetry D(5) broken to bilateral D(1)
      Day Lily: it and many other monocot flowers have symmetry D(3), weak D(6)
      Daffodil: monocot; symmetry D(3), close to D(6)

    2. Discrete 2D space groups: wallpaper groups

      The 17 wallpaper groups (Wikipedia) are discrete groups with translational grid-based symmetries. They also have grid-preserving rosette-group symmetries. They can be extended into three dimensions as the 80 layer groups.

      Fish scales: scales often have symmetry cm: rhomb/rect-ctr + bilateral D(1)
      Honeycomb: made by honeybees, with symmetry p6m: hexagonal + D(6)

  3. Three-Dimensional Symmetries

    1. 3D point groups: crystallographic

      Point groups in three dimensions. These come in two types: prismatic or axial, and Platonic or quasi-spherical.

      Prismatic, axial:

      Rel. Frieze Refl Discrete (n-fold) Continuous
      p111 C(n) SO(2,planar)
      p11m X C(n,h) SO(2,planar)*O(1,axial)
      p11g X S(2*n) SO(2,planar)*O(1,axial)
      p1m1 X C(n,v) O(2,planar)
      p211 D(n) O(2,planar-axial)
      p2mm X D(n,h) O(2,planar)*O(1,axial)
      p2mg X D(n,d) O(2,planar)*O(1,axial)

      The rosette-group examples here are 2D projections of C(n) and C(n,v).

      Platonic, quasi-spherical:

      • Tetrahedral: T, Th, Td
      • Octahedral: O, Oh
      • Icosahedral: I, Ih
      • Continuous: SO(3), O(3)

      In order,

      1. Name
      2. Version with rotations only (chiral)
      3. Version with reflections made by multiplying rotations by -1 (inversion)
      4. Version with other sorts of reflections (tetrahedral only; all the other shapes are inversion-symmetric)
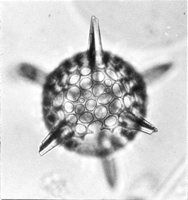
      Hexacontium enthacanthum radiolarian: octahedral symmetry Oh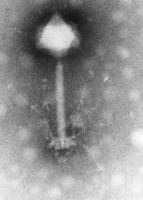
      S-PM2 bacteriophage: many viruses have icosahedral symmetry Ih

    2. Discrete 3D space groups: crystallographic groups

      The 230 crystallographic space groups are a 3D version of the wallpaper groups, with translational grid-based symmetries and grid-preserving point-group symmetries. Plant tissues, like wood, are sometimes close enough to regular to approximately fit some of these groups.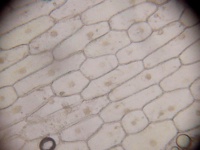
      Onion cells: semiregular gridlike pattern

  4. Fractal Symmetries

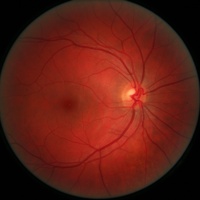
    A fractal is a self-similar object with a self-similarity dimension that need not be an integer. Starting at scale L, construct a new scale, L/n, that is smaller by n. Count the number of times N that the scale-L/n version of the object appears in the scale-L version. The fractal dimension D one finds from N = n^D. Approximate fractals appear in branched structures of organisms like tree branches, blood vessels, air vessels, sap vessels, etc.
    Human retina: the blood vessels have a fractal dimension around 1.7
    Reference: Fractal analysis of the vascular tree in the human retina. [Annu Rev Biomed Eng. 2004] - PubMed result

The images are courtesy of contributors to Wikimedia Commons and Flickr, though they were cropped and rescaled as appropriate. They follow the licensing appropriate for derivative works of the originals.

To my symmetry index page